Based on Adam Touré, Martin Trépanier, and Thierry Warin’s upcoming paper
As trade policy discussions around the upcoming trilateral review of CUSMA heat up, the focus often narrows to bilateral trade deficits and surpluses. However, a new working paper from our lab reinforces the notion that looking at trade through a simple transactional lens misses the structural integration of the North American economy.
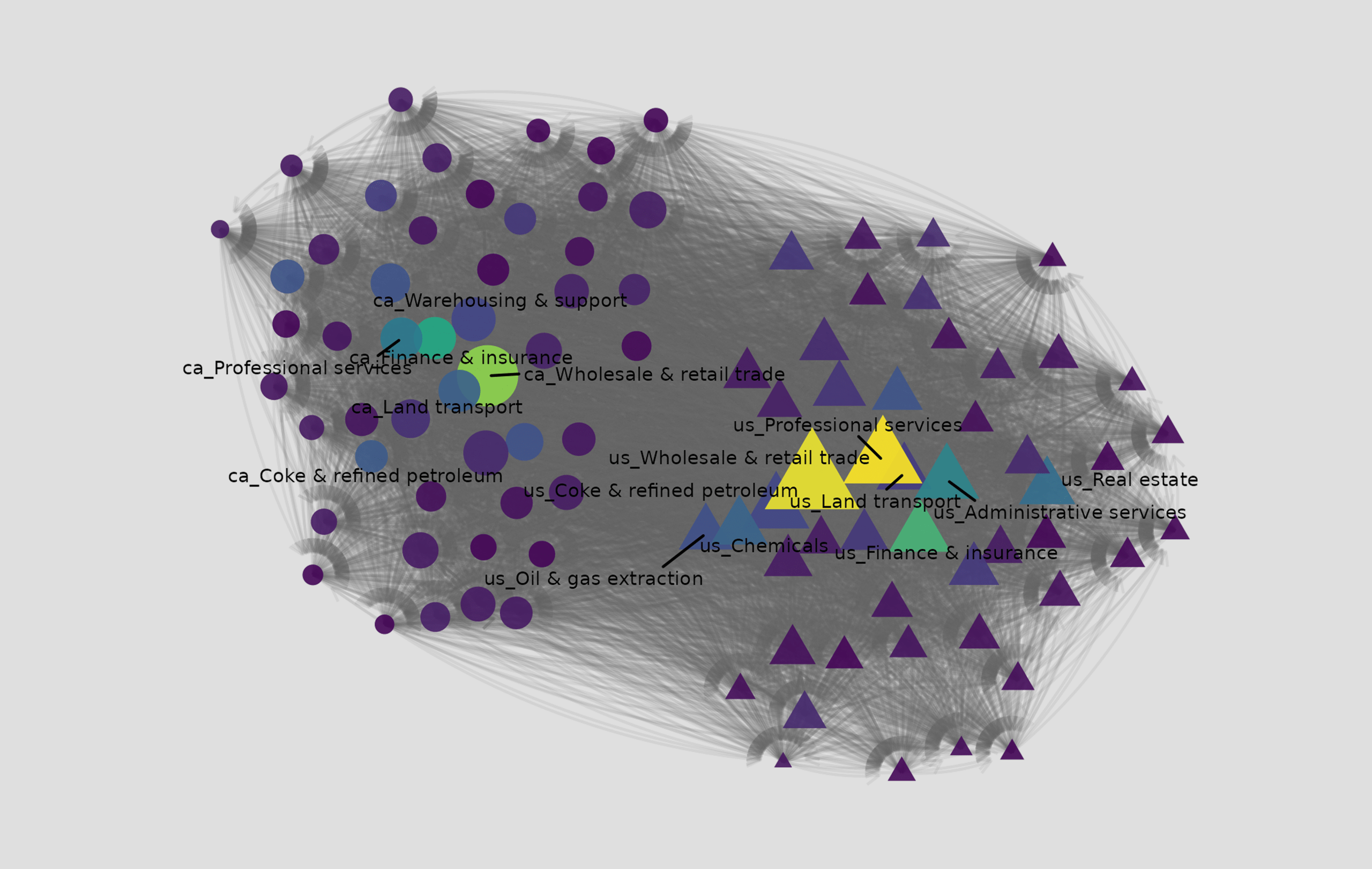
Touré, Trépanier, and Warin apply network science to OECD’s 2022 inter-country industry input-output tables to study the Canadian and American economies as a closed network. By assigning industries as nodes and their input-output flows as edges, the authors reveal the nervous system of this shared economy.
The economies of the two countries are an interdependent mesh
Traditional trade data treats the administrative boundaries of a country as separate buckets through which firms buy and sell goods. The network structure built using IO data reveals a different reality. We see two dense clusters where Canadian and American industries are inextricably linked.
The visualization shows that there is no clean border in the economic network. Instead, we see an interdependent ecosystem with two cores. Canadian industries are more closely connected with each other than with the American ones, and the same is true in the other direction. Yet industries in both of these cores have a vast number of connections between each other. This suggests that protectionist measures aimed at a specific foreign industry are likely to ripple back and impact domestic sectors due to these dense cross-border bridges.
The service-based systemic core
A crucial pattern emerges in the study’s analysis of the network using the metrics of Random Walk Centrality and Counting Betweenness. The industries in the top-right quadrant act as the systemic core. While we often focus on manufacturing in trade disputes, the chart identifies US Professional Services, Finance & Insurance, and Administrative Services are the dominant industries in the network.
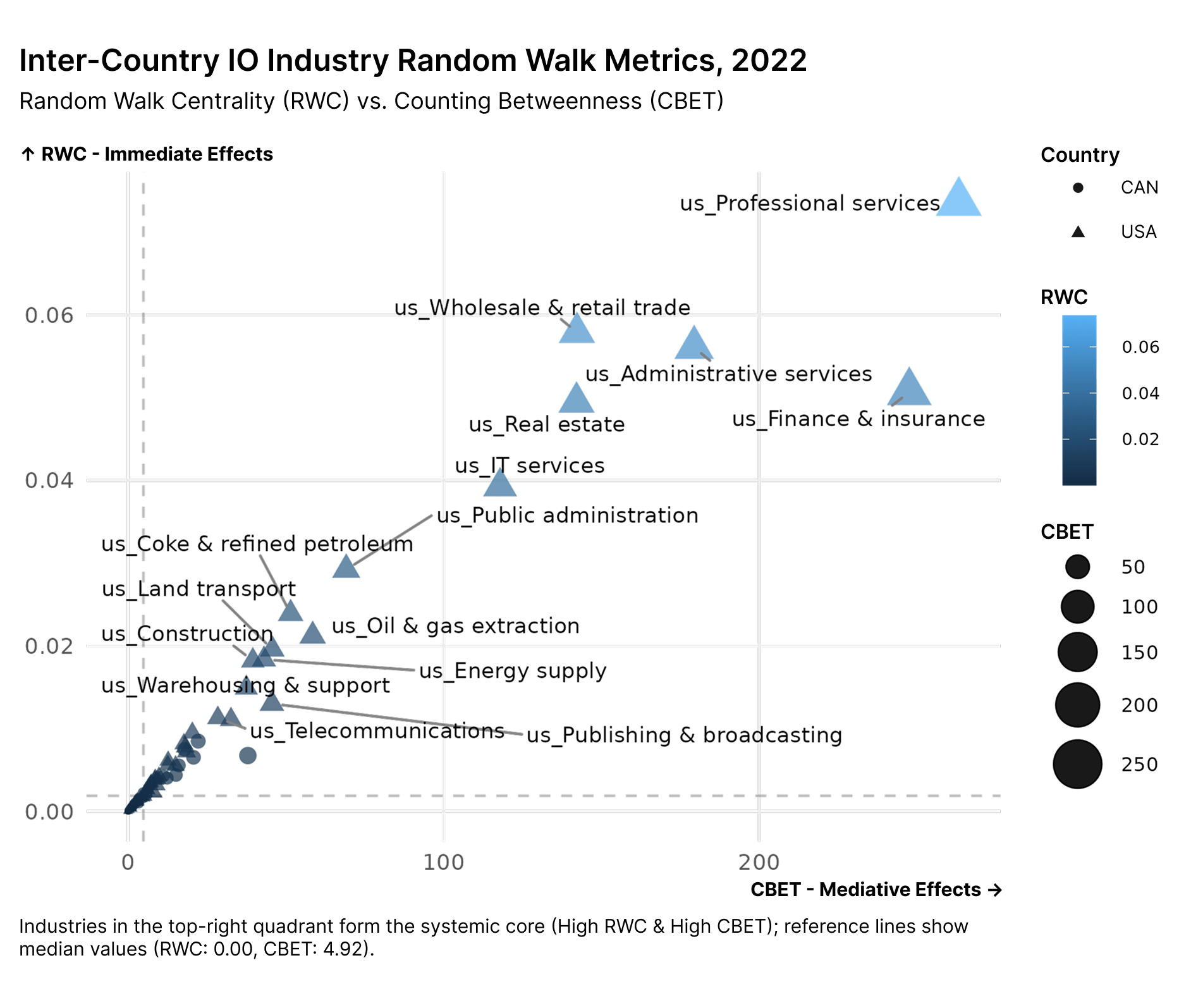
Industries with high Random Walk Centrality exert immediate and massive direct effects on the economy. Meanwhile, those with high Counting Betweenness act as bridges or super-connectors through which the vast majority of economic activity flows.
This highlights a shift from a manufacturing-centric view of trade to a service-centric one. Professional services are not just a sector but rather the infrastructure upon which the manufacturing and resource trades rely to function. Disrupting the flow of goods invariably strains the service network that manages those flows.
Strength relies on integration
The analysis of Out- and In-Strength also reveals interesting insights. Industries that are major suppliers to the network (as a proportion of their total output) have the largest out-flow to in-flow ratio as shown by the Influence Index. Meanwhile, the largest importing industries in the network are not always major suppliers but are more goods-based than service-based. Unlike the previous metric where US industries play a relatively larger role, this metric shows that Canadian industries also have a dominant position in the network.
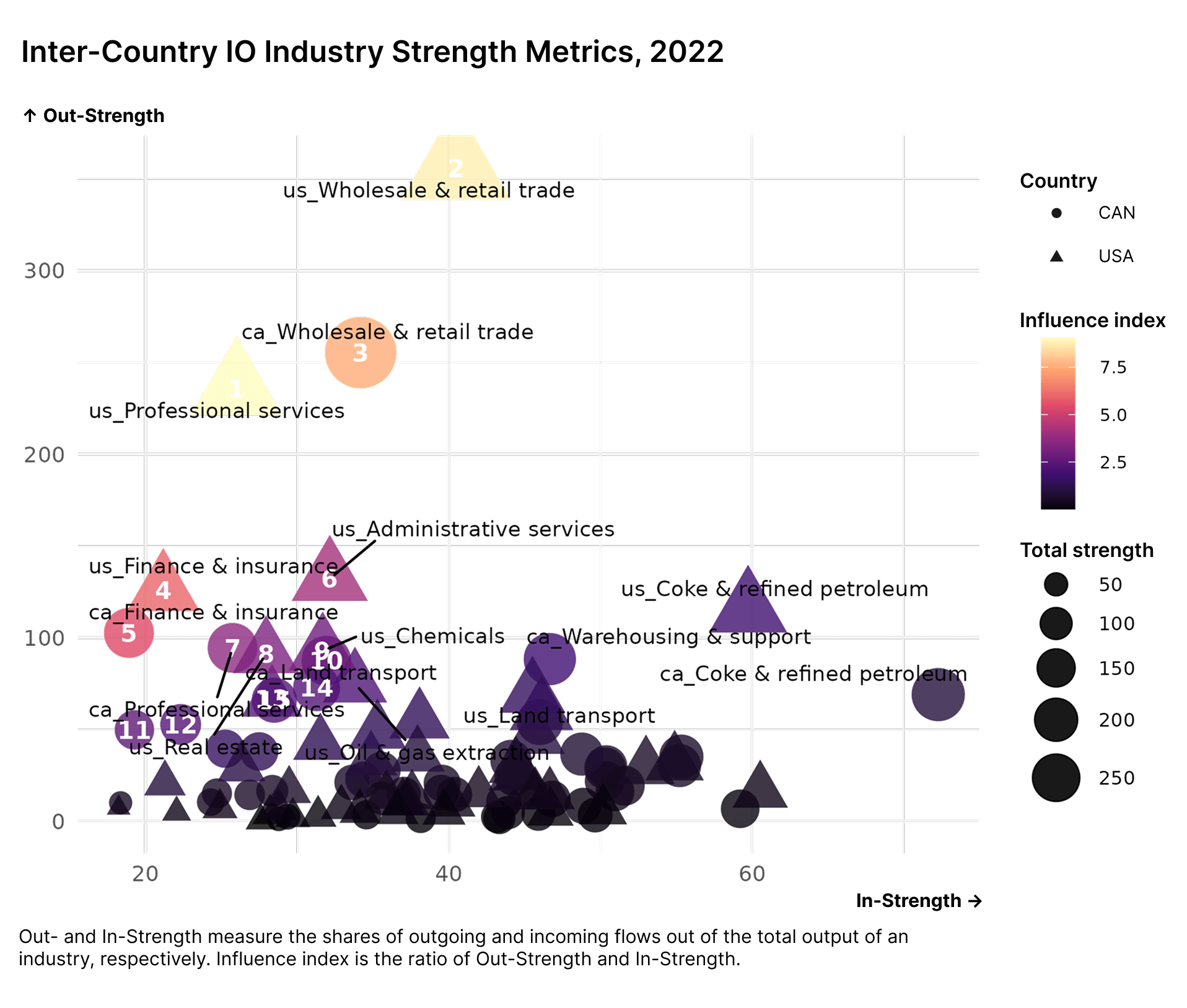
Notable nodes like US Wholesale & Retail Trade and CA Wholesale & Retail Trade sit at the top of this hierarchy. This indicates that the most influential players in our shared economy are service-based and distributional in nature. They aggregate inputs and distribute them to the wider economy. The analysis shows that one cannot isolate a strong exporter without acknowledging their dependence on the network for inputs.
Implications for the CUSMA review
The analysis suggests that the CAN-USA economic relationship has evolved beyond simple partnership into structural interdependence. The Influence Index calculated in the paper indicates that separating these economies would not be a clean surgical procedure but rather a disruption of a single and shared organ system.
As policymakers navigate current tensions, this network perspective offers a sober reminder that there are no isolated events in a system this tightly coupled.